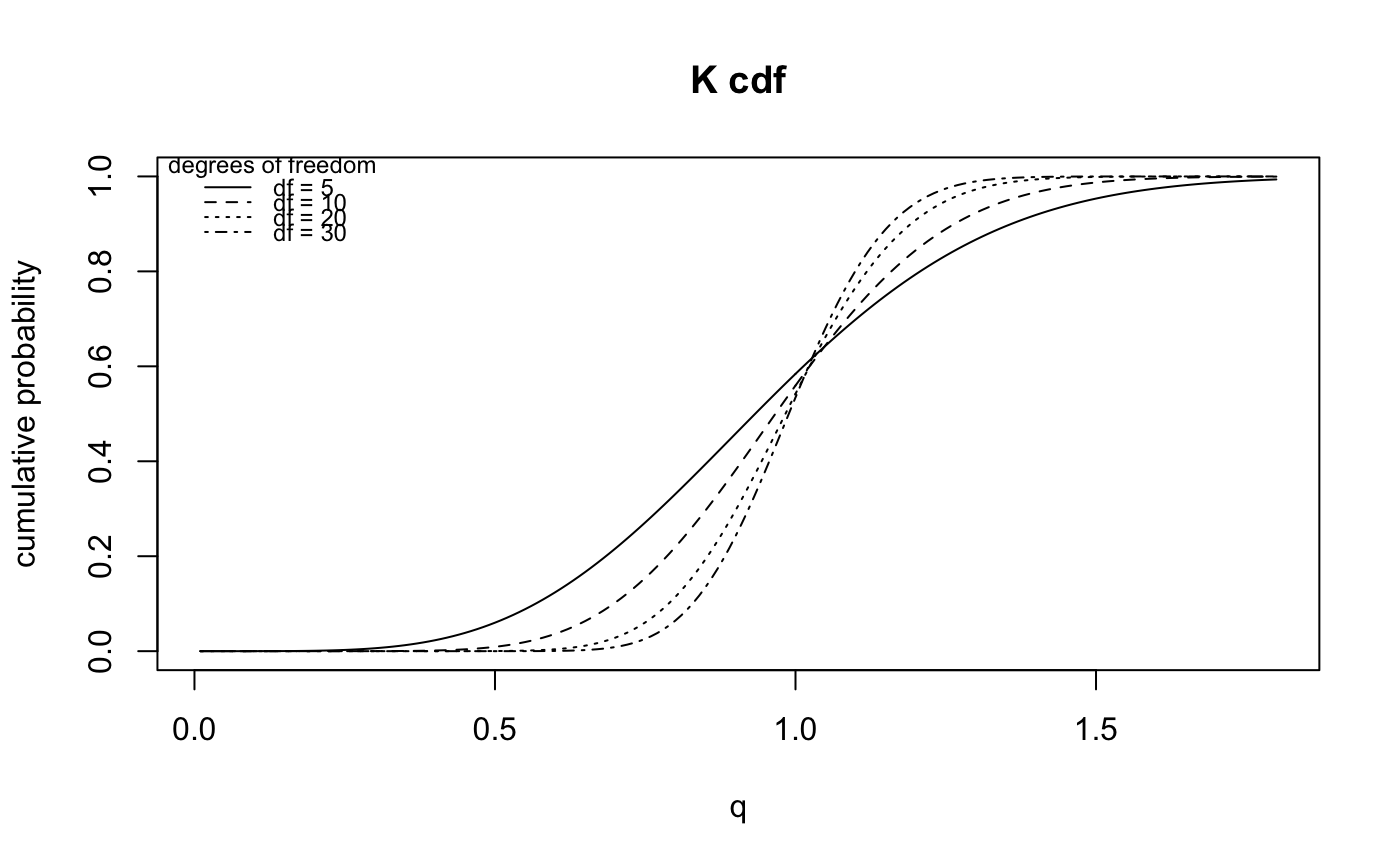
pkay The cumulative distribution function K distribution

Source: R/pkay.R

The cumulative distribution function for the K distribution on df degrees of freedom having non-centrality parameter ncp.

A K distribution is the square root of a chi-square divided by its degrees of freedom. That is, if x is chi-squared on m degrees of freedom, then y = sqrt(x/m) is K on m degrees of freedom. Under standard normal theory, K is the distribution of the pivotal quantity s/sigma where s is the sample standard deviation and sigma is the standard deviation parameter of the normal density. K is the natural distribution for tests and confidence intervals about sigma. K densities are more nearly symmetric than are chi-squared and concentrate near 1. As the degrees of freedom increase, they become more symmetric, more concentrated, and more nearly normally distributed.

pkay(q, df, ncp = 0, upper.tail = FALSE, log.p = FALSE)

Arguments

q

A vector of quantiles at which to calculate the cumulative distribution.
df

Degrees of freedom (non-negative, but can be non-integer).
ncp

Non-centrality parameter (non-negative).
upper.tail

logical; if TRUE, instead of returning F(q) (the default), the upper tail probabilities 1-F(q) = Pr(Q>q) are returned.
log.p

logical; if TRUE, probabilities are given as log(p).

Value

pkay returns the value of the K cumulative distribution function, F(q), evaluated at q for the given df and ncp. If upper.trail = TRUE then the upper tail probabilities 1-F(q) = Pr(Q>q) are returned instead of F(q).

Invalid arguments will result in return value NaN, with a warning.

The length of the result is the maximum of the lengths of the numerical arguments.

The numerical arguments are recycled to the length of the result. Only the first elements of the logical arguments are used.

Note

All calls depend on analogous calls to chi-squared functions. See pchisq for details on non-centrality parameter calculations.

Examples


pkay(1, 20)
#> [1] 0.5420703
q <- seq(0.01, 1.8, 0.01)
#
# Plot the cdf for K(5)
u <- pkay(q,5)
plot(q, u, type="l",
     xlab="q", ylab="cumulative probability",
     xlim=range(q), ylim=c(0,1),
     main="K cdf")
#
# Add some other K cdfs
lines(q, pkay(q,10), lty=2)
lines(q, pkay(q,20), lty=3)
lines(q, pkay(q,30), lty=4)
legend("topleft",
       legend=c("df = 5", "df = 10", "df = 20", "df = 30"),
       lty=c(1,2,3,4),
       title="degrees of freedom",
       cex=0.75, bty="n")

#
# See the vignette for more on the "K-distribution"
#