rkay The K distribution - generating pseudo-random values

Random generation for the K distribution on df degrees of freedom having non-centrality parameter ncp.

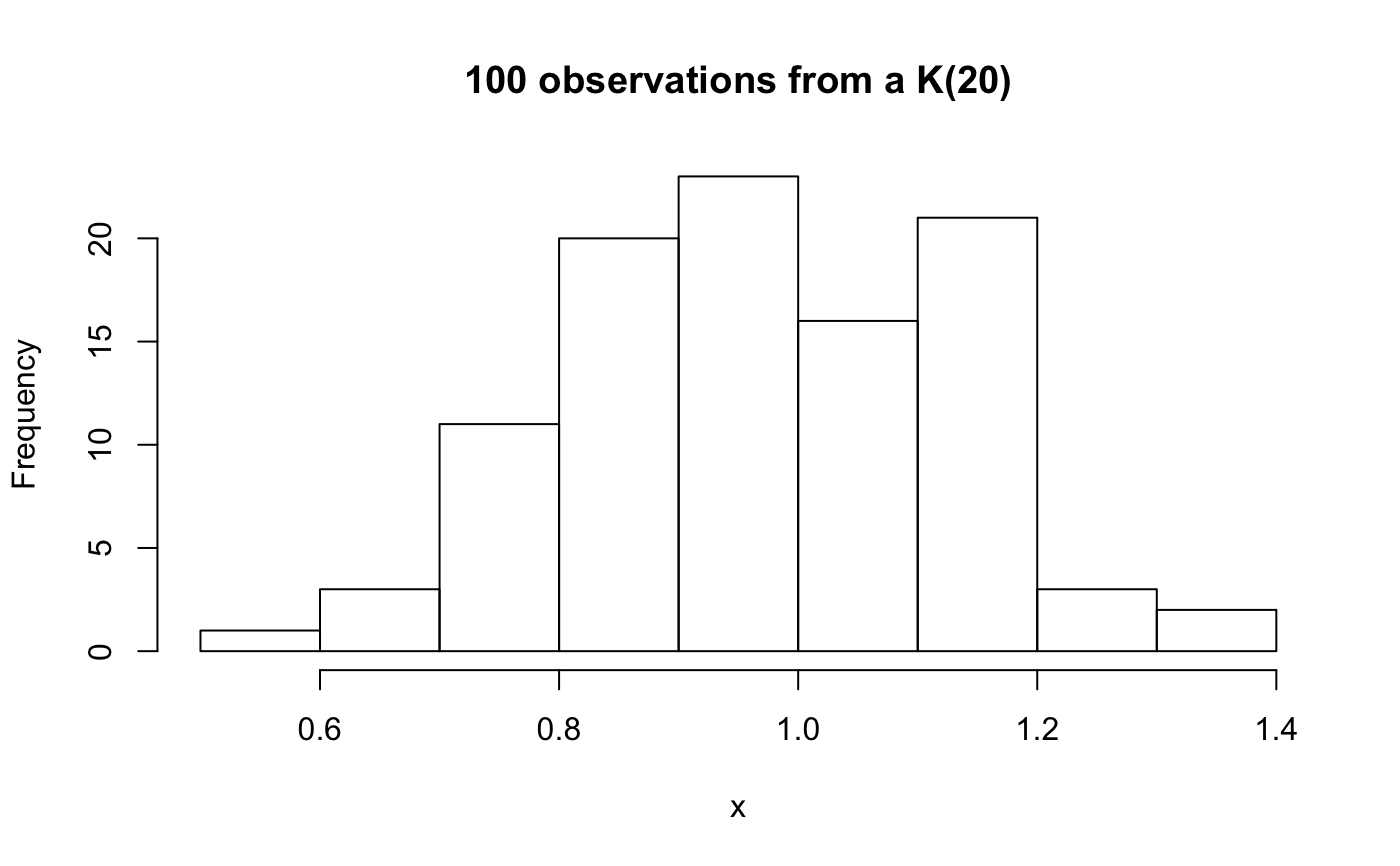
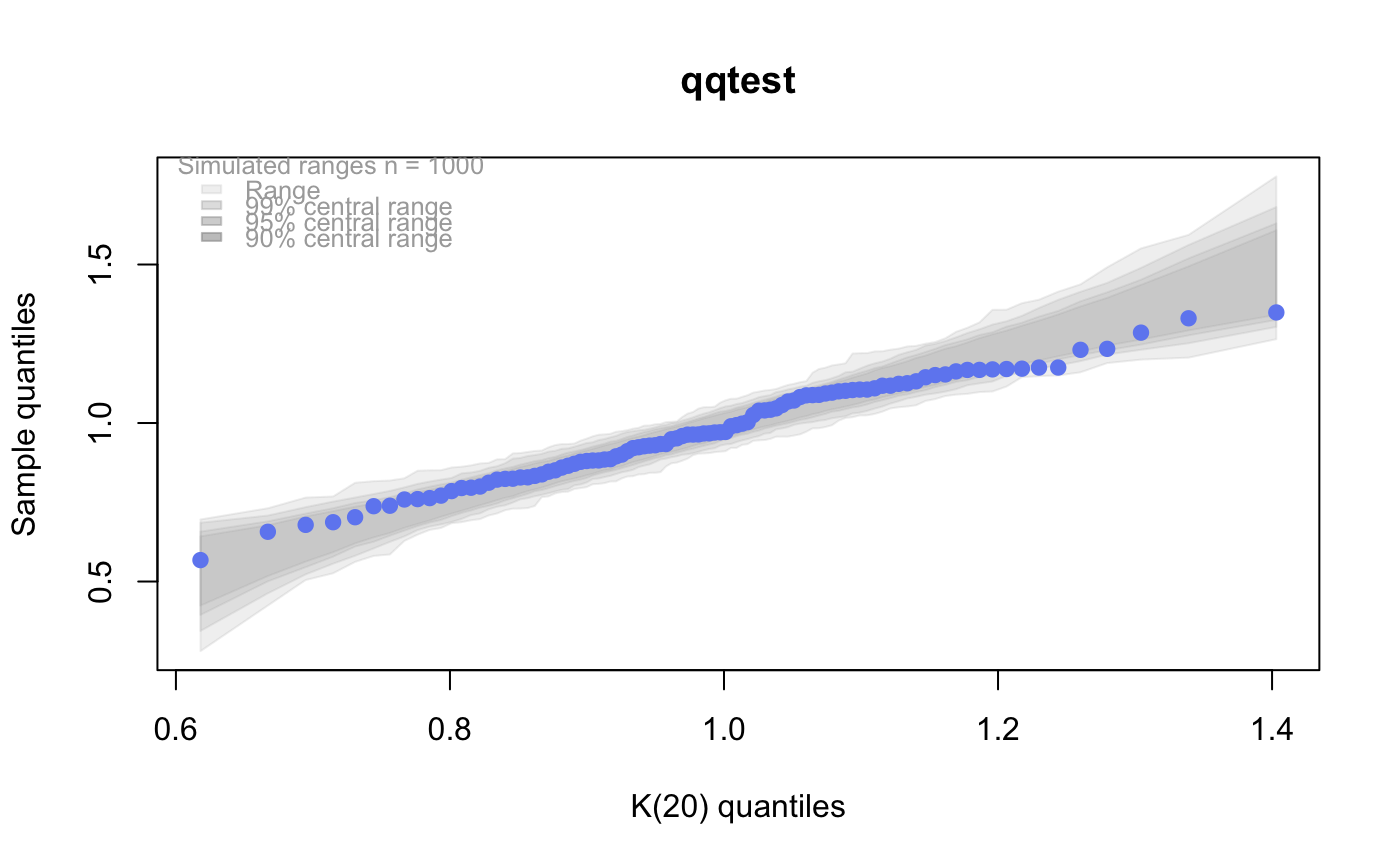
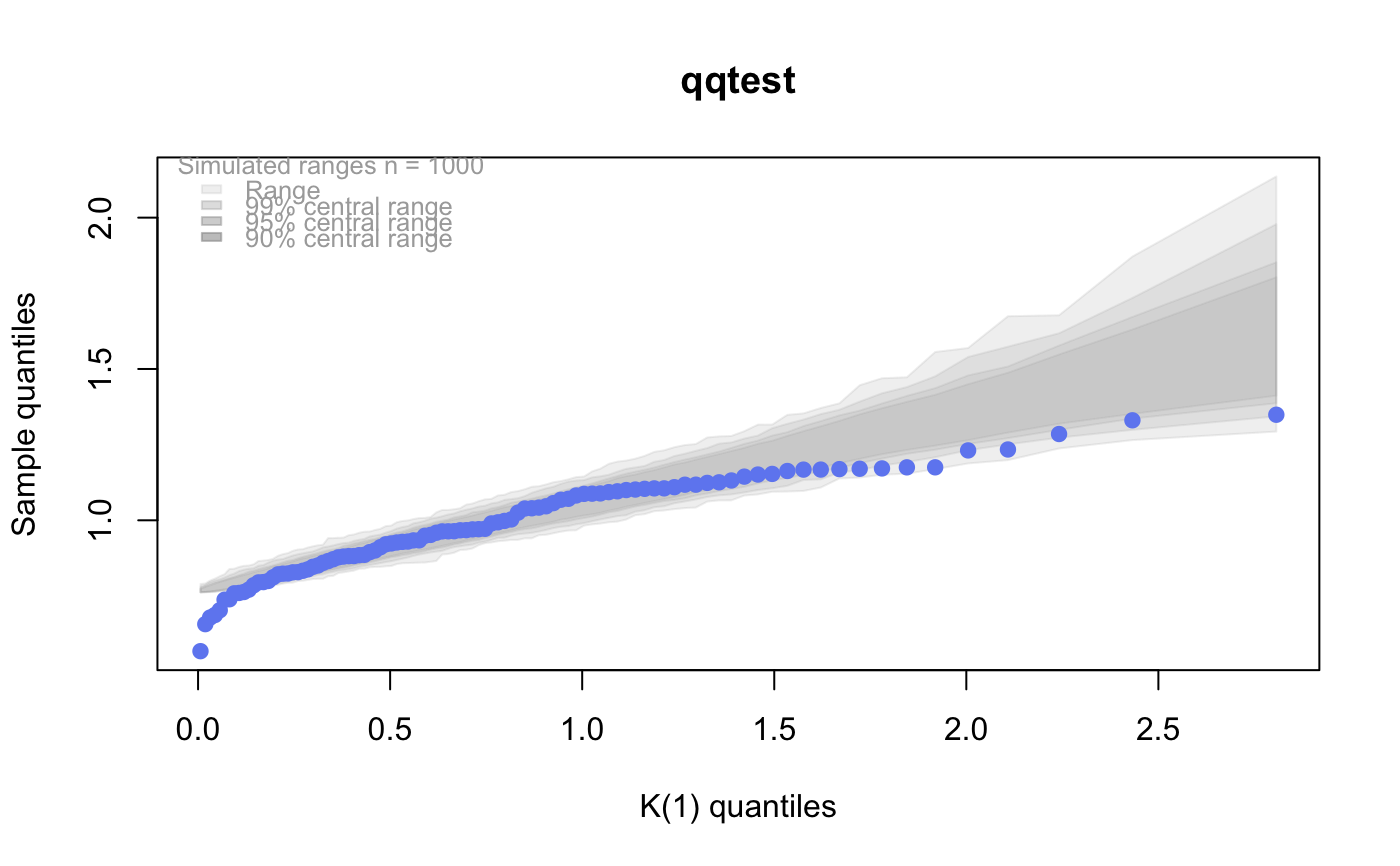
A K distribution is the square root of a chi-square divided by its degrees of freedom. That is, if x is chi-squared on m degrees of freedom, then y = sqrt(x/m) is K on m degrees of freedom. Under standard normal theory, K is the distribution of the pivotal quantity s/sigma where s is the sample standard deviation and sigma is the standard deviation parameter of the normal density. K is the natural distribution for tests and confidence intervals about sigma. K densities are more nearly symmetric than are chi-squared and concentrate near 1. As the degrees of freedom increase, they become more symmetric, more concentrated, and more nearly normally distributed.

rkay(n, df, ncp = 0)

Arguments

n	Number of observations. If length(n) > 1, the length is taken to be the number required.
df	Degrees of freedom (non-negative, but can be non-integer).
ncp	Non-centrality parameter (non-negative).

Value

rkay returns pseudo-randomly generated values.

Invalid arguments will result in return value NaN, with a warning.

Note

Depends on call to analogous chi-squared functions. See rchisq for details on non-centrality parameter calculations.

Examples

x <- rkay(100, 20)
hist(x, main="100 observations from a K(20)")
# Certainly looks like it comes from a K on 20
qqtest(x, dist="kay",df=20)
# for this many degrees of freedom it looks
# a lot like a gaussian (normal) distribution
qqtest(x, dist="gau",df=1)
# But not like it came from a K on 1 degree of freedom
qqtest(x, dist="kay",df=1)
#
# See the vignette for more on the "K-distribution"
#